今天我們要來簡單聊聊邏輯回歸(Logistic Regression)，簡單來説，邏輯回歸雖然名字中有「回歸」，但它其實是一個分類算法，特別擅長處理二分類問題，並且邏輯回歸可以通過擴展來處理多分類問題，例如使用 Softmax 函數進行多分類。雖然它不能直接處理線性不可分的問題，但它能給出樣本屬於某一類的概率。

邏輯迴歸是一種資料分析技術，使用數學來尋找兩個資料要素之間的關係，並根據其中一個要素預測另一個要素的結果。這樣的預測通常具有有限數量的結果，例如是或否。

線性可分

邏輯回歸的原理是通過在數據集中找到一條可以將樣本分為兩類的直線（在高維空間則是一個超平面，Hyperplane ）。這樣的數據集被稱為「線性可分」的數據集。

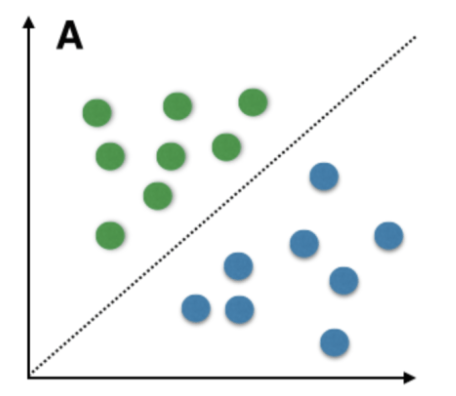
假設我們有兩類樣本，分別用 +1 和 -1 表示。如果存在一個權重向量(w)和一個偏置(b)，使得對於所有樣本(x)：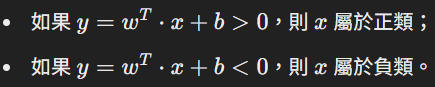

那麼這個數據集就是線性可分的。這裡的(T) 表示的是對權重向量(w) 的轉置操作。

Sigmoid 函數

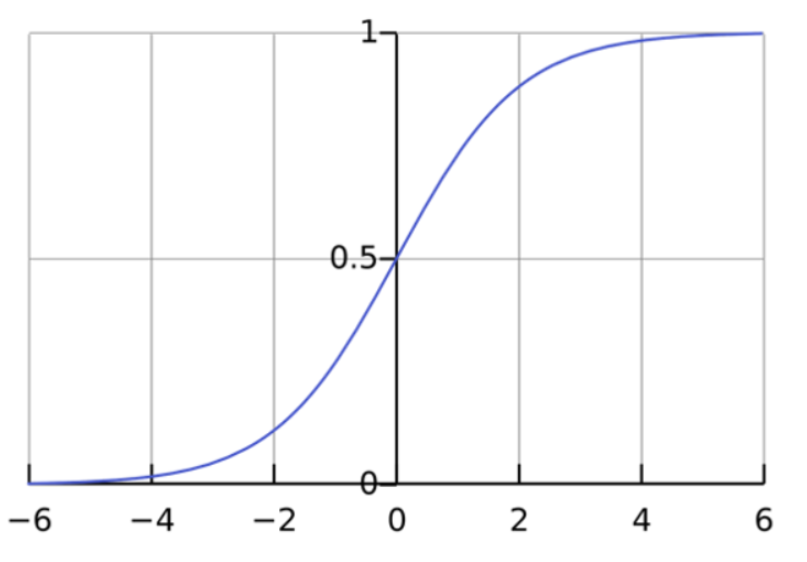
在上一章才介紹過的Sigmoid函數，我們先來復習一下Sigmoid函數是什麽：
Sigmoid函數在邏輯回歸中用來將線性輸入映射到一個介於 0 和 1 之間的概率值。這使得邏輯回歸可以對輸入樣本進行概率估計，並進一步決定樣本屬於哪一類。

Sigmoid 函數的數學表達式如下：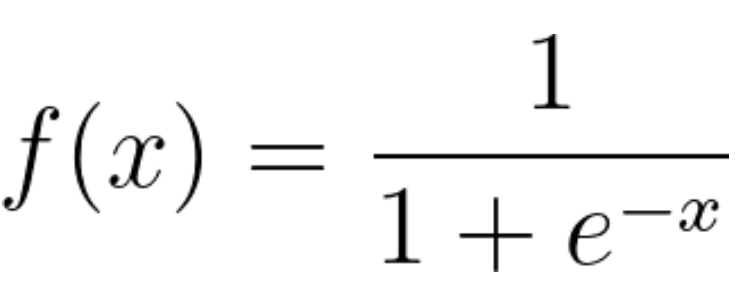

當輸入值(x)趨近於負無窮時，輸出值接近 0；當(x)趨近於正無窮時，輸出值接近 1。這樣，邏輯回歸的模型就可以將輸入值轉換為概率，從而判斷樣本屬於某一類的可能性。